Using Logic for

Building Correct Software

What is an incorrect program?

---

Assertions

Recall the idea of the state of a program:

A state is an assignment of a value to each variable in the program.

 

e.g. If the variables are x,y,z,ip

is a state.

specifies

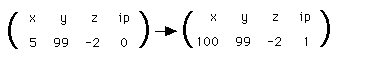
among an infinite number of other transitions

Typical assertions are attached to points between statements.

Attaching an assertion does not make the assertion true.

Assertions which are always true are called invariants.

Starting states of interest are specified by assertions, which we call

input assertions

or possibly

assumptions.

---

Example

We claim the intermediate and ouptut assertions shown are

invariant relative to the input assertion n > 5.

by induction of some form.

Two main principles:

transition induction :

induction on # of transitions made to get to state

structural induction :

induction on data domain

Basis: Assertion is true the first time we get to this point.

Proof of basis We see that n>5 and x==0 the first time. So x + n > 5n > 0.

Induction Step: Assume assertion is true now, show it will be true next time.

The induction step is

We see

---

Summary of What is to be Shown

one typically

assumes H,

tries to derive C.

From 3 & 4, 6 is equivalent to

(x + 1) + (n - 1) > 5

Which is equivalent to

x + n > 5

Which is exactly assumption 1.

QED

From 4, this is equivalent to

which follows from 5 (n > 5, assuming n integer ).

follows from the intermediate assertion

The verification condition is

(we don't need primes, since no changes.)

implies

n == 0

Combining this with x + n > 5

we get

x > 5

QED

is called a loop invariant.

 

Loop invariants are the key stepping stone between input and output assertions.

----initialization----

while( ----condition---- )

{

----body----

}

Note that going around the loop leaves the quantity

x + n

unchanged.

Make the initial assertion:

Use as the invariant in the loop:

true since

x == 0

n == n₀

n₀ > 5

Induction step

x + n does not change

n₀ does not change

n > 0 to go around loop

so n > 0 after decrementing 1

Exit

mean that n == 0

since x + n == n₀

x == n₀ on exit, and n₀ > 5.

• If a loop invariant asserts too much, there may be too much to be shown,

  e.g. from the input assertion.

• If it asserts too little, there may not be enough assumable

  to complete the induction.

---

Exercise

Identify the most informative loop invariant in the following:

s == j²

Induction:

Basis : First time s == 0, j == 0

s == j² is true

Induction Step :

s == j² s' == j'²

where

s' == s + k

j' == j + 1

Can't be shown, because there is no restriction on k.

s == j²k == 2j + 1

Basis: (you do it)

Induction Step: To show

[ s == j²k == 2j + 1s' == s + kj' == j + 1k' == k + 2 ]

[ s' == j'²k' = 2j' + 1 ]

s + k == (j+1)²k + 2 = 2(j+1) + 1

follows from

s == j²k == 2j + 1

Working forward from the latter:

QED

More importantly, the loop usually is trying to establish some output assertion. Knowing that assertion helps tune the loop invariant.

Often, we can work backward from the output assertion to get the invariant.

s == n²

i.e. the purpose of the program was to compute n² without using multiplication.

If not, strengthen it so that adequacy is achieved.

If the input assertion is true when the program starts,

then the output assertion will be true when & if the program ends.

This is called Partial Correctness because it does not establish that the program will terminate.

wrt an input assertion

means

partial correctness

+

termination whenever we start in a state with that assertion.

Here is one technique that can be used:

An energy function is a function

e: States{0,1,2,3,...}

such that on any two successive visits to the loop point s^*s'

e(s) > e(s')

i.e. the energy has decreased.

Reason:

e(s) > e(s') > e(s'') > ...

cannot continue forever, since e has a minimum value of 0.

can be viewed as a kind of

checks & balances

activity.

The specification checks the program, the program checks the specification.

Developing such abstractions is similar in many ways to

functional & logic programming.

The latter can be viewed as hybrids between programs and specifications.