Your name __________________________
Harvey Mudd College
CS 60 Final Exam
Spring semester, 1996
Open book and notes
3 hours
8 problems
8 pages
Provide solutions to the attached problems directly on these pages. It is suggested that you look over the exam first to get an idea of how to apportion your time. Work so as to maximize total points. Do not get stuck on one problem at the expense of others.
The exam is given under the conditions of the HMC honor code. During the exam, you may refer to any of your own reference materials, but consulting with others or using their materials is forbidden.
1. [5 points]
Suppose a binary relation knows among people is given in Prolog. From this relation, show the definition in Prolog of another binary relation linked as follows: Person P is linked to person Q if either both P and Q know some person, or if one of them knows someone who is linked to the other.
2. [15 points]
Note: Problem 3 is related to this problem. You will want your answer to this problem to be clean, so that you will be able to analyze it in problem 3. Avoid using append and reverse, since these may make complexity analysis in problem 3 more difficult.
For purposes of searching, it is desired to restructure an ordered list into a tree which is as balanced as possible but maintains the same left-to-right order as the original list. “Balanced” in this case means that the two sub-trees of any interior node have heights which differ by at most 1 from each other. For example, list
[1, 2, 3, 4, 5, 6, 7, 8, 9]
would be restructured into
[ [ [1, 2], [3, 4] ], [ [5. 6], [7, [8, 9] ] ]
Present the rex definition of a function balance which accomplishes such a structuring. (Note: applying balance to a list of one element yields the element.) You will probably want to use one or more auxiliary functions. Define any ones which are not written up in the course materials.
Suggestion: To split the list, use two separate functions rather than a single function which returns a pair of lists. This will make it easier to understand and analyze.
3. [15 points]
Derive a “O” upper bound for the time required by your program in problem 2 on a general list of length N. (Assume that first, rest, and cons, or their corresponding list-matching counterparts, are O(1).) Justify your answer carefully; do not guess.
4. [15 points]
Consider the following C++ code for binary search of an ordered array of length N. It returns an index at which the sought element occurs in the array, or -1 if the element does not occur.
template <class T> long binary_search(T array[], long N, T sought) { long low = 0, high = N-1;while( /* invariant */ low <= high ) { long midpoint = (low + high)/2;if( array[midpoint] == sought )return midpoint; // foundif( array[midpoint] < sought )low = midpoint + 1; // search upperelsehigh = midpoint - 1; // search lower }return -1; // not found }
Provide a descriptive and convincing loop invariant which shows that binary search really works. State why your invariant leads to the function giving the correct answer in the case that the sought element does not occur in the array.
5. [15 points]
Consider the following fragment of C++ code:
typedef int logical;logical p, q, r, s;p = P(); q = Q(); r = R(); s = S();if( ( !p && !q && !r) || (q && !r && s) || (!p && r && s) || (p && !q && s) )foo();
Simplify the if statement as much possible, given that you also know both of the following:
q will never be 0 if p == 0 and r == 1 and s == 0
p will never be 1 if q == 1 and r == 1 and s == 1.
6. [15 points]
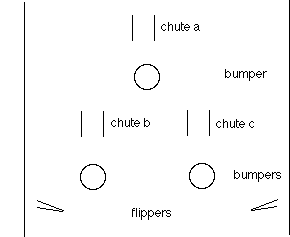
A tricky pin-ball game has three chutes a, b, and c as shown below. Every time the ball goes through the chutes in the sequence a b a c, the player accrues a bonus. For example, in the chute sequence a b a a b a c b a b a c b a bonus would be accrued twice.

Construct a finite-state acceptor which accepts the overall chute sequence every time a bonus is merited. What regular expression describes the acceptor? Implement the acceptor using sequential logic. Specifically, encode the state using flip-flops and specify the next-state equations for each flip-flop.
7. [10 points]
Suppose we wish to add a new feature to the video game Walris. This new feature is called “cloning”. The clone command produces a copy of the selected shape, following the original shape by a few pixels, provided that there is sufficient space to do so. The idea is that if the player thinks it will be helpful, she can clone the shape to fill a wall faster. Once a shape is cloned, the select key rotates selection among all moving shapes on the screen. Another shape can thus be cloned or, if the clone is moved, the original shape can be cloned a second time.
.............................................................. . # 2222 . . ### . . ##### . . 3 * # . . 3 * . . 3 * . . 3 * . ..............................................................Modified Walris game: The selected (*'ed) shape has been cloned, creating shape 3.
Describe qualitatively what internal changes would need to be made to the game to accommodate cloning. What object-oriented ideas are used in cloning? How will the game keep track of the additional shapes? How does the updating process in the event loop change? Use code fragments to help explain your ideas.
8. [10 points]
Despite its elegance, the ISC architecture contains some redundancy, in the sense that some instructions could be implemented in terms of others. Show why the following are redundant by giving a sequence of other instructions which accomplishes the same effect:
a. copy R S // copy the value in S into Rb. aim R V // add immediate value V to register Rc. jsub R S // jump to the address in register R,// leaving the next address in register Sd. and R S T // bit-wise AND the contents of registers S and T// and store the result into R
Note: The instruction pointer register IP is not directly accessible to the programmer and cannot be specified as a register index.