Your name __________________________
Harvey Mudd College
CS 60 Final Exam
Fall semester, 1995
Open book and notes
3 hours
7 problems
11 pages
Provide solutions to the attached problems directly on these pages. It is suggested that you look over the exam first to get an idea of how to apportion your time. Work so as to maximize total points. Do not get stuck on one problem at the expense of others.
The exam is given under the conditions of the HMC honor code. During the exam, you may refer to any of your own reference materials, but consulting with others or using their materials is forbidden.
1. [5 points]
a. Give rex rules for defining the function bit, where bit(i, N) is the ith least-significant bit of the binary representation of natural number N, counting bit 0 as the least significant bit.
Your solution should not use the following unnecessary devices: lists, arrays, logarithm function. Keep it simple.
b. Give rex rules for precisely defining the function num_bits, where num_bits(N) is the minimum number of bits required to represent natural number N in binary.
2. [20 points]
Consider the Towers of Hanoi puzzle introduced early in the course. Suppose we wish to construct a C++-style object-oriented simulator for a generalized version of this puzzle. The generalization is in the number of spindles allowed (the traditional puzzle has three spindles; we allow N).
Give the code for the salient points of such a simulator. Assume that spindles are numbered 0, 1, 2, ...., N-1, and that the disks are similarly numbered, with smaller disks having smaller numbers. The key method for class puzzle is
move(int i, int j)
which moves a disk from spindle i to spindle j. The constructor for a puzzle has as arguments the number of spindles and number of disks. The puzzle should make use of other classes rather than reinventing them, if possible. Any of the classes discussed during the course or which appear in the notes may be used.
Do not worry about a graphic display; simply show the state of the game by printing out on the disks on each spindle.
3. [15 points]
Consider the following C++ code:
// assert X == X0polylist L = X;polylist R = NIL;while( /* */ !null(L) ){R = cons(first(L), R);L = rest(L);}// assert reverse(R) == X0
Here reverse denotes the usual list reversal function. Note that we can apply reverse to both sides of the equality in the final assertion to get R == reverse(X0), since for any list R, reverse(reverse(R)) == R. In other words, we are asserting that this code reverses the original list.
a. What loop invariant would you assert at /* */ in order to establish that the final assertion follows from the initial assertion? (You may make use of the function append in your loop invariant.)
If you are utterly stuck on coming up with the invariant, you can "buy" the invariant for 5 points, to give yourself the chance to complete the problem. If you do this, please write "bought invariant" in the space above. The invariant can be bought from me. It is not permissible to pass on a bought invariant to others taking the exam.
b. Give an argument which shows that the final assertion follows from the loop invariant.
c. Give an argument (e.g. using primed and unprimed variables for before and after the loop body) which shows that the loop invariant really is invariant.
4. [15 points]
Give tight "O" time bounds, as a function of the value of N, on for the program fragments below. (Note: As a statement i /= 2; means the same thing as i = i / 2;.) Unless otherwise stated, assume single arithmetic operations are O(1).
fragment a:
int i, j;for( i = N; i > 0; i /= 2 )for( j = i; j > 0; j-- ).... some O(1) computation ....
fragment b:
int i, j;for( j = N; j > 0; j-- )for( i = j; i > 0; i /= 2 ).... some O(1) computation ....
fragment c:
double F = 1;for( i = N; i > 0; i-- )F *= N;
fragment d: (Extra credit)
Same as fragment c, except assume that multiplications require time proportional to the product of the number of digits in the numbers being multiplied.
5. [10 points]
Suppose the time complexity t(n) of an algorithm is c*n, where c is a constant. Suppose that t0 is the running time for a certain n, n0. If we double the input size, we get a running time of c*2n0 = 2t0. So we can start a table which expresses t(2n0) in terms of t0 with the first line below. This table is interesting because it gives an intuitive idea of how the time complexity grows when the input size is doubled. For example, for some complexities doubling the input size entails multiplying the time by a certain constant, and for others it is better or worse than this.
Algorithm time complexity t(n0) t(2n0) comment cn t0 2t0 O(n) c t0 O(1) cn2 t0 O(n2) cn3 t0 O(n3) cnk, k a constant t0 O(nk) c log n t0 O(log n) c n log n t0 O(n log n) c 2n t0 O(2n)
The problem is to fill in the missing entries in the table by doing analyses similar to that for the first row.
6. [20 points]
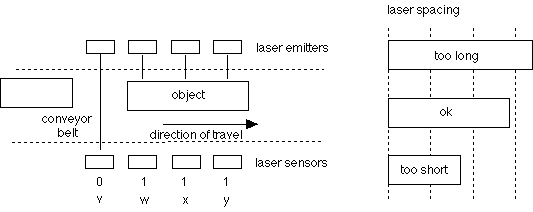
A conveyor belt monitor is shown schematically below. The purpose of the monitor is to reject objects which are either too long or too short. A properly-sized object is defined as one which can break no more nor fewer than three of the four equally-spaced laser beams at one time. If an object breaks all four of the beams, it is considered too long. If it breaks fewer than three of the beams, it is considered too short. Assume that the objects are spaced far enough apart on the belt, in relation to the sample rate, that we don't get false registrations resulting from a following object combining with an object to get a false reading of four beams being broken.

The array of four sensors v, w, x, y detects whether a beam is received or not. These emit logic values of 1 if the beam is broken and 0 if it is not.
a. [5 of 20 points] List the combinations vwxy which should cause object rejection. Then plot those combinations on a Karnaugh map. (Note: Combinations such as 1100 should not cause rejection, since this might just represent the first part of an entering ok object.)
b. [10 of 20 points] P.D. Quick notices that, rather than causing a rejection, the combinations 0010 and 1010 could be treated as "won't occur" or "don't care", since objects creating those patterns would have been rejected earlier (e.g. as 0100). Will this observation result in any net simplification of the logic function for object rejection? Explain why or why not.
c. [5 of 20 points] How many different 4-argument switching functions are there anyway (universally, not specific to this problem)?
7. [15 points]
Referring to the previous problem, I.M. Smart thinks he has found a way to reduce the costly replication of lasers and sensors by using sequential logic. Assuming that a clock can be kept in synchronism with the belt travel rate, Smart suggests that a single laser-sensor pair can be used. The single sensor transmits a 1 or a 0 to a finite-state machine on each clock tick. (The clock will tick three times during the interval in which an ok object travels past.) The following diagram indicates the sequence transmitted to the finite-state machine from when an ok object is first sensed.
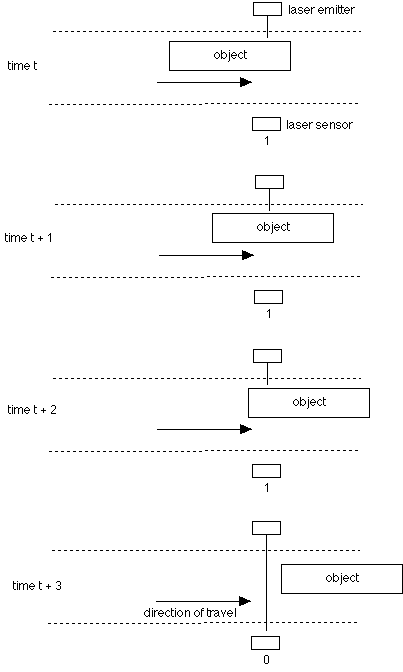
a. [5 of 15 points] Give the state-transition diagram for a finite-state machine which will determine whether an object should be rejected (for any sensor sequence, not just the example one above). [Despite the sound of it, is probably simplest if this machine is in the form of a transducer rather than a classifier, i.e. that the output is associated with transitions rather than states, since the decision to reject occurs based on a combination of state and input. Thus the output on each transition is either reject R or nothing _. However, representing the machine as a classifier is also possible if you want to do it that way.]
Hint: Start with a state assuming the conveyor is clear of any objects. Then track what can happen next.
b. [10 of 15 points] What is the minimum number of flip-flops necessary to implement the finite-state machine? Chose a sufficient number of flip-flops and a state encoding. Then derive the logic equations for each flip-flop based on that encoding. Use variable x to refer to the input sensor value. Do not worry about providing the logic equations for the output.
Note: Even if you are not certain about your answer to part a, you can get credit for properly implementing your answer to it (assuming your answer is not too distant).