Your name __________________________
Harvey Mudd College
CS 60 Final Exam
Fall semester, 1996
Open book and notes
3 hours
7 problems
8 pages
The exam is given under the conditions of the HMC honor code. During the exam, you may refer to any of your own reference materials, but consulting with others or using their materials is forbidden.
Provide solutions to the attached problems directly on these pages. It is suggested that you look over the exam first to get an idea of how to apportion your time. Work so as to maximize total points. Do not get stuck on one problem at the expense of others.
The action items in each problem are shown in bold-face.
Use the back of the previous page if you need more space for a given problem.
1. [15 points]
Construct function pick in the programming language of your choice.
pick(Goal, Items)
where Goal is a non-negative integer and Items is a sequence of positive integers, yields a pair. The first element of the result pair is the sum of the elements in the second element, as defined next. The second element of the pair is a set of integers in Items which has a sum (there many be more than one) that is closest to Goal without exceeding it, where each item can be used at most once. For example,
pick(4, [1, 8, 3, 5]) ==> [4, [1, 3]]
pick(10, [1, 8, 3, 5]) ==> [9, [1, 8]] ([9, [1, 3, 5]] is also acceptable)
pick(0, [1, 8, 3, 5]) ==> [0, []]
In the first example, 1+3 == 4 exactly. In the second, 1+8 == 9, the closest we can come to 10 with the numbers given. In the third case, choosing the empty list sums to 0 exactly.
Your construction should be succinct and readable, for one reason because you will be asked to analyze its complexity in the next problem.
2. [10 points]
Give a tight "O" upper bound on your solution to problem 1. Use as the problem size, N, the number of elements in the list of items. Assume that addition and subtraction of two numbers takes constant time.
3. [15 points]
Using the Java class Vector, we wish to construct a new class SortedVector. This class provides method ElementAt so that for any index I, the value of ElementAt(I) is the I-th smallest value in the vector. To simplify the discussion, the ordering used to define smallest is assumed to be given by some fixed static method not shown. Class SortedVector also provides AddElement(Ob) which adds object Ob to the vector. There are at least two conceivable strategies for implementing SortedVector:
(a) sort-on-insertion strategy: The vector is always maintained in sorted order. When a new element is inserted, it is inserted in the proper place.
(b) sort-on-demand strategy: When elements are added, they are just added to the end of the vector. Sorting takes place when, and only when, ElementAt is called the first time since the previous AddElement was called. Thus unnecessary sorting is avoided.
Present Java code for the implementation of SortedVector using strategy (b). Code the class declaration and the following methods:
void AddElement(Object X) // add an element to a SortedVectorObject ElementAt(int I) // get Ith element of a SortedVector
Recall that class Vector implements the following methods:
void addElement(Object X) // add X to the end of the vectorObject elementAt(int I) // select element at index Iint size() // return number of elements
You may assume existence of a static method Sort which you do not have to code. Assume that Sort sorts the vector in place.
4. [15 points]
Consider the familiar program for quicksort shown below. What is the appropriate loop invariant for the for loop which is essential in establishing correctness of the program? Give an English-language description before attempting to use predicate logic.
void quicksort(T a[ ], long low, long high) { if( low >= high ) return;T pivot = a[(low + high)/2];long i = low-1; long j = high+1;for( ; ; ) { do { i++; } while( a[i] < pivot );do { j--; } while( a[j] > pivot );if( i >= j ) break;exchange(a[i], a[j]); }quicksort(a, low, i-1); quicksort(a, j+1, high); }
5. [20 points]
Dingbat Controls Corp. has supplied the following thermostatic controls used in the Olin Building. Each control has two buttons, one labeled + the other labeled -. The buttons can be pressed individually, or both simultaneously. The function of this control is supposed to allow variation of temperature +/- 3 degrees from a setpoint stored in a central computer. Pressing + alone increases the temperature one degree, and pressing - decreases it one degree. Three degrees above the setpoint, pressing + has no effect. Neither does pressing - three degrees below. Pressing + and - simultaneously resets the temperature to the setpoint. (Assuming the control is sampled synchronously, if neither button is pressed, the state is not changed.)
Part a [5 of 20 points]. Model this control as a finite-state classifier, assuming that the state and output values are -3, -2, -1, 0, +1, +2, +3 indicating degrees from the setpoint. Show the state-transition diagram. The input alphabet is {+, -, +}.
Part b [15 of 20 points]. Assume that state and output values are coded in "two's complement" binary and that the inputs are coded thus:
state and output inputu v w x y -3 1 0 1 + 0 1 -2 1 1 0 - 1 0 -1 1 1 1 + 1 1 0 0 0 0 1 0 0 1 2 0 1 0 3 0 1 1
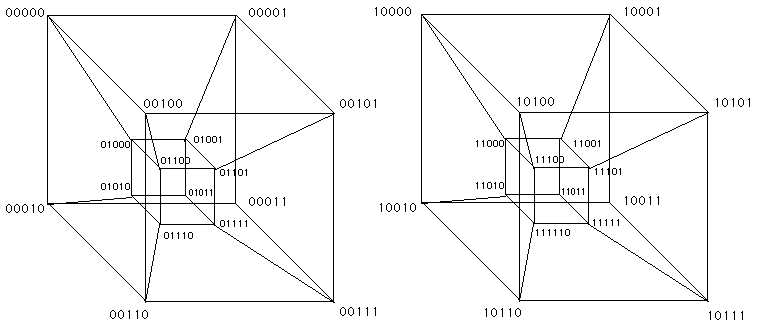
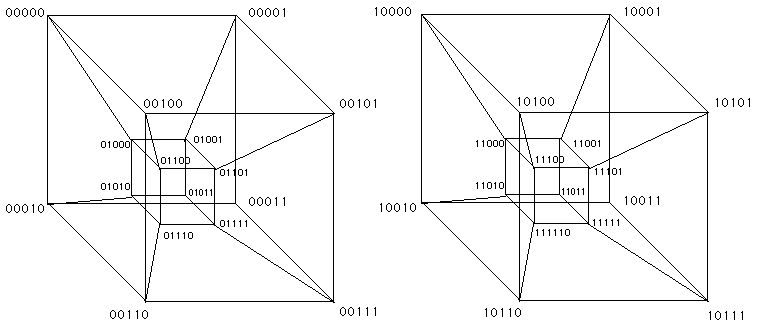
Plot the minterms for the next-state function for variable v (the second state variable) on the 5-dimensional hypercube shown on the next page by darkening vertices for which the next value of v is 1. Also, plot by marking an X for any don't care combinations. Then give a simplified expression for the next-state value of v. Adhere to the variable ordering uvwxy in the hypercube labeling, so that I will know what you mean. (In order to prevent cluttering in the five-dimensional hypercube, cross-edges between the two major hypercubes are not shown.)
(problem 5 continued)

Here's a second copy of the 5-dimensional hypercube in case you need it:
6. [15 points]
"R expressions" (not to be confused with "regular expressions") is the name we have given to the nestable structures used in rex, for example [1, [2, 3, [ ] ], 4, [5] ]. (Note: An atom by itself is considered an R expression too; that is, not every R expression is a list.) Assuming that a grammar, with start symbol A, already exists for defining the atomic elements of R expressions (such as numerals), express a grammar for R expressions themselves. Use R as the start symbol for this grammar. Don't forget to handle the commas. Based on your grammar, sketch the construction of a parser which recognizes R expressions. Assume that a parser for atomic strings already exists. Assume methods get and peek for getting the next character from the input and peeking at it, respectively. Note: By "sketch" we mean that you do not have to worry about setting up all the Java class structure, etc.; just express the main idea.
7. [10 points]
Based on what you know about computer structure, why is a switch statement preferable to a long sequence of if statements in performing a conditional execution based on the value of an integer variable? Under what circumstances would it not be preferable? How could the idea of hashing be used to alleviate the problem in the latter case?