Note: In using this to help prepare for the midterm in any given semester, please keep in mind that the material covered in your semester might differ somewhat from that covered when this exam was given.

Your name __________________________

Harvey Mudd College

CS 60 Mid-Term Exam

Fall semester, 1994

Five Problems

Open book and notes

Please provide answers to the problem groups directly on these pages. It is suggested that you look over the exam first to get an idea of how to apportion your time. Work so as to maximize total points; do not get stuck on one problem at the expense of others.

During the exam, you may refer to any of your own reference materials, but consulting with others or using their materials is forbidden.

When code is requested, exhibiting the correct idea is more important than syntactic precision.

The answers to these problems need not be exceptionally long. Please think through your solution before you plunge into a long exposition that might not address the main point of the question.

1. [20 points]

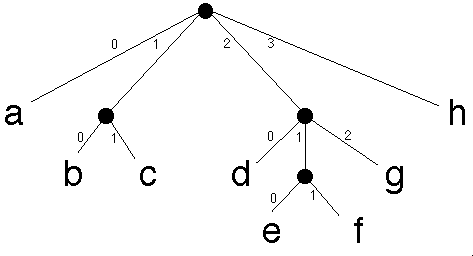
As you know, trees can be represented as lists in a variety of ways. Consider the representation in which a multi-ary tree is represented as nested lists, with the leaves of the tree corresponding to atoms in the list. For example,

A multi-ary tree, represented by the list [a, [b, c], [d, [e, f], g], h].

The numbers are simply intended as a visual guide; they are not part of the tree proper.

Assume that all leaves have distinct labels. By the tree address of a leaf, we mean a list of numbers that will direct us to the particular leaf. The interpretation of successive numbers in this list tells us which branch to take (counting from 0). For example, here are some tree addresses in the above tree:

leaf		tree address 

a 			[0] 

b 			[1, 0] 

c 			[1, 1] 

e 			[2, 1, 0] 

Similarly, we can extend this idea to the tree address of sub-trees:

sub-tree 	tree address 

[b, c] 			[1] 

[e, f]			 [2, 1] 

Present the formal definition (e.g. using rex or similar language) of a function find_node which will take two arguments, a tree and a tree address, and return the corresponding sub-tree rooted at the corresponding node. Assume that a leaf actually exists at the address given, i.e. do not worry about error-checking. For example, if T is the tree above, then

find_node([2, 1, 0], T) ==> e

find_node([2, 1], T) ==> [e, f]

etc.

2. [20 points]

Continuing with the previous tree representation, present the formal definition of a function find_address which will take as its arguments a tree and a node and return the tree address of the node. If there is no corresponding node, this function should return 0 (which is distinguishable from a valid address since it is not a list). For example, if T is the tree above, then

find_address(e, T) ==> [2, 1, 0]

find_address([e, f], T) ==> [2, 1]

3. [20 points]

An electronic mail address consists of a user name followed by an @ character, followed by a host identifier, followed by some number of domain identifiers, each separated by periods. For example:

keller@muddcs.cs.hmc.edu 

Give both a grammar and a syntax diagram for such addresses. Assume the identifiers are just constructed of lower case letters (no numbers or special characters).

4. [20 points]

Sketch code for a parser that will parse addresses of the form in problem 3, returning a list of the identifiers used therein. The user name should be last, followed by the domains in the reverse order of their appearance, then the host. For the example given, the resulting list should be

( edu hmc cs muddcs keller ) 

Do not replicate definitions used in class handouts, discussions, or homework you've submitted. Simply refer to them and say what they do. Do not worry about whitespace.

5. [20 points]

For this problem, a sparse array is conceptually a large two-dimensional array in which a large fraction of the entries (say 95% or more) are 0. A problem which often arises entails viewing such an array as a set of coefficients of linear forms, with an eye toward computing the value of the form. For example if the array were:

a₀₀ a₀₁ a₀₂ .... a_0,n-1

a₁₀ a₁₁ a₁₂ .... a_1,n-1

a₂₀ a₂₁ a₂₂ .... a_2,n-1

....

a_m-1,0 a_m-1,1 a_m-1,2 .... a_m-1,n-1

and we are given a one-dimensional array of values x0, x1, ...., xn-1, we want to compute the m values:

y₀ = a₀₀x₀ + a₀₁x₁ + a₀₂x₂ + .... + a_0,n-1x_n-1

y₁ = a₁₀x₀ + a₁₁x₁ + a₁₂x₂ + .... + a_1,n-1x_n-1

....

y_m-1 = a_m-1,0x₀ + a_m-1,1x₁ + a_m-1,2x₂ + .... + a_m-1,n-1x_n-1

In the present case of interest, both m and n are on the order of 10,000, so storing a full two-dimensional array, with its attendant 100,000,000 elements, has prohibitive memory requirements.

As an alternative, we are willing to store the x and y values as a linear array, but wish to store the coefficients as an array of lists. Sketch how you would represent the data to enable computing the linear forms in C++. Give whatever declaration code you need in order to be convincing that this can be done in C++. Don't sketch the actual computation.

&127;