Your name __________Answers___________
Harvey Mudd College
CS 60 Mid-Term Exam
Fall semester, 1997
Five Problems
100 Points
Closed book
Instructions
During the exam, the only item to which you may refer is your own reference sheet, 1 double-sided sheet of 8.5" x 11" paper.
The exam is planned for 1 hour, 15 mins., ending at 4:00 p.m. You may use the time from 4:00-4:15 if the classroom is not otherwise in use, but all papers must be in by 4:15 at the latest.
Please provide answers to the problem groups directly on these pages. It is suggested that you look over the exam first to get an idea of how to apportion your time. Work so as to maximize total points; do not get stuck on one problem at the expense of others.
When code is requested, exhibiting the correct idea is more important than syntactic precision. However, keep your definitions clean and readable. Use the clearest program structure possible.
The answers to these problems should not be exceptionally long. Please think through your solution before you plunge into a long exposition that might not address the main point of the question.
1. [30 points]
A census taker wishes to create an information structure for collecting information about neighborhoods. Here is the model used:
A Neighborhood consists of:a mail (e.g. Zip) codeA Household consists of:
a set of Householdsan addressA Person consists of:
a set of Personsa name
a birthdate
an occupation
Assume that all atomic quantities (ones which are not further decomposed) are of type String.
a. [5 points] Show the form of an information structure which could be used for an entire Neighborhood (e.g. using rex lists, and ... type notation).
ans:
Neighborhood = [mailCode, H1, H2, H3, ...., Hm], where each Hi is a Household
Houshold = [address, P1, P2, ...., Pn] where each Pj is a Person
Person = [name, birthdate, occupation]
b. [5 points] Show the overall type of the Neighborhood information structure. (Recall, for example, that A* designates the type of an arbitrarily-long list of elements of type A, A ´ B is the type of a pair consisting of an A and a B, etc.)
ans:
String x(String x(String xString xString)*)*
c. [10 points] If you were coding the full Neighborhood structure in Java (with all the constituent components), what class definitions would you use? (Just show the data declarations, not constructors or methods.) Include classes you would use for the sets. Be thorough enough to be convincing.
ans:
class Neighborhood
{
String mailCode;
HouseholdList households;
}
class Household
{
String address;
PersonList persons;
}
class Person
{
String name;
String birthdate;
String occupation;
}
class HouseholdList
{
Household First;
HouseholdList Rest;
}
class PersonList
{
Person First;
PersonList Rest;
}
d. [10 points] When a new child is born in a neighborhood, it is desired to add the child to the representation by a method of Neighborhood:
newChild(Address, Name, Birthdate)
Assuming the occupation of a new child is "baby", sketch how the newChild method would work. The result does not have to be runnable code, but it should be readable pseudo-code (combination of code and English).
ans:
In class Neighborhood:
void newChild(String address, String name, String birthdate)
throws NoSuchAddressException
{
// find the household using address
Household found = find(address, households);
if( found == null )
throw new NoSuchAddressException();
Person person = new Person(name, Birthdate, "baby");
// add the new person to the list of the household found
found.PersonList = PersonList.cons(person, found.PersonList);
}
Household find(String address, HouseholdList list)
{
while( list != null )
{
if( HouseholdList.first(list).address.equals(address) )
return HouseholdList.first(list);
list = HouseholdList.rest(list);
}
return null;
}
2. [20 points]
A mathematician desires a function which will determine empirically whether binary operators (functions) are associative over a set of values. A binary function b is said to be associative over a set S if for every way of drawing X, Y, and Z from S, it must be true that
b(X, b(Y, Z)) == b(b(X, Y), Z)
Assuming the set S is represented by a list, implement the function isAssociative so that isAssociative(b, S) will tell whether or not b is associative over S. For example, we expect the results
isAssociative(+, range(1, 10)) ==> 1
isAssociative(-, range(1, 10)) ==> 0
Use higher-order functions, such as map, in conjunction with other high-level functions such as pairs (where pairs(L, M) produces all ordered pairs, the first element from L and the second from M. You do not have to write the code for pairs. In fact, you do not even have to use pairs; it's just one to approach the problem.)
Once you have settled on the expression for isAssociative, give a clear statement in English of how it works.
ans:
isAssociative(b, L) =
all((X) => all((Y) => all((Z) => b(X, b(Y, Z)) == b(b(X, Y), Z), L), L), L);
The statement is "forall X in L, forall Y in L, forall Z in L,
b(X, b(Y, Z)) == b(b(X, Y), Z)"
We just translated the statement into rex. The definition of all is that all(P, L) is 1 iff every element of L satisfies P, and 0 otherwise.
alternate answer:
// checkTriple checks one triple of values [X, Y, Z] to see if the equation
// b(X, b(Y, Z)) == b(b(X, Y), Z);
// for that triple holds (by returning 1 or 0 respectively)
checkTriple(b, T) =
[X, Y, Z] = T,
b(X, b(Y, Z)) == b(b(X, Y), Z);
// b is associative if checkTriple is true for all triples T.
isAssociative(b, S) = all((T) => checkTriple(b, T), triples(S));
// triples(L) gives all triples [X, Y, Z] where X, Y, and Z are elements of L.
// pairs(L, pairs(L, L)) gives all pairs of the form [X, [Y, Z]] and
// leaves([X, [Y, Z]]) gives [X, Y, Z], so mapping leaves gives us the
// list of triples in the desired form.
triples(L) = map(leaves, pairs(L, pairs(L, L)));
pairs(L, M) = mappend((X) => map((Y) => [X, Y], M), L);
3. [20 points]
Consider the function redmap which composes the higher-order functions reduce and map according to the following definition:
redmap(B, Unit, F, List) = reduce(B, Unit, map(F, List));
Here B is a binary function and F is a unary function. Assume that the types match up appropriately. Using the above definition has the disadvantage that an intermediate list (the result of map) is created when none is actually required, since that list is immediately reduced by reduce.
Give a low-level (i.e. inductive or recursive) definition of redmap from first principles (e.g. using rex rules). Your definition should not incur the disadvantage of intermediate list construction.
ans:
redmap(B, Unit, F, []) => Unit;redmap(B, Unit, F, [A | L]) => B(F(A), redmap(B, Unit, F, L));
4. [15 points]
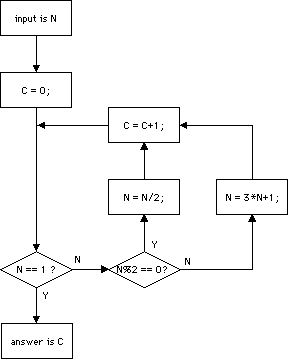
Use McCarthy's transformation to create a recursive (e.g. rex) program from the following flowchart. Call the function of this program f.

ans:
f(N) = g(N, 0);g(1, C) => C;g(N, C) => N%2 == 0 ? g(N/2, C+1);g(N, C) => g(3*N+1, C+1)
5. [15 points]
A technique used to solve puzzles such as Gradual Insanity is to invent macro operators, sequences of moves which cause certain large-scale rearrangements to take place. A trivial example for Gradual Insanity is a macro operator which rotates all columns one position to the right. Or, one might try to discover a macro operator which transposes two columns while leaving other colors as they were at the start of the macro. Learning such a set of macro operators is one of the standard ways for solving Rubik's cube, for example.
Suppose we have Java class Pattern which implements the basic moves as methods. We wish to create a new class macroPattern which contains all the basic moves, plus selected macro operators. Contrast the approaches of inheritance vs. embedding in creating the new class, where by embedding we mean that the new class contains a variable of the original class which contains the pattern. Note that you are not being asked to code the macro operators, just to show the two structural approaches.
ans:
With embedding, the class macroPattern contains a variable of class Pattern . For any of the basic operators, such as setAll (which sets all colors) we would like macroPattern to have, we would have to create new methods which call the corresponding method of class Pattern. With inheritance, this is unnecessary; macroPattern automatically has those methods. In code, we would have:
embedding:
class MacroPattern { Pattern p; void setAll(Color c) { p.setAll(c); } .... other basic operators .... .... macro operators .... }
inheritance:
class MacroPattern extends Pattern { .... macro operators .... }
Because it entails more code to create and maintain, embedding is more error-prone. With inheritance, we can pass a MacroPattern as an argument to any method requiring a Pattern. This is not true with embedding; we'd have to specify which type of argument more precisely.
Possible Optional Extra Credit: If you feel that you could not adequately respond to one or more questions on this exam, you may use this page to expound on your knowledge of some other aspect on which you feel particularly well-prepared but which was not addressed. In this, you are limited to the material in the first seven chapters (i.e. excluding grammars and parsers) of the notes. For example, you might feel that you have a thorough grasp of Turing machines or infinite lists and can write about them in your own words. This offer only applies to course-related material, not other outside material that you may know. This extra credit can be used to bring your total score up to 100 points, but not to exceed that.
ans:
What can I say? This is a great deal.