Discussed so far:
Transducers:
input sequence -> output sequence
Now:
Classifiers:
input sequence -> finite set of classes
Acceptors:
Classifier with just 2 classes
A classifier
is not viewed as producing a
sequence:
instead it classifies the input into one of a finite set of classes:
A class is associated with each state;
(The same class may be associated with more than one state.)
Example
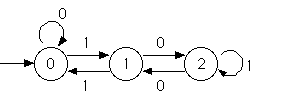
Classify binary input MSB first into class mod3 :
There are 3 classes {0,1,2}

e.g.
0
1
10
11
100
101
110
111
1000
1001
1010
1011
1100
1101
1110
:
:
:
An acceptor is a classifier with only 2 classes
Examples
Acceptor for binary numerals MSB first which are divisible by 3.
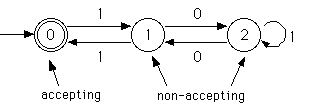
Acceptor for sequences containing at least 3 1's:
A graphical tool:
Java Formal Languages & Automata Pkg
Prof. Susan Rodger
Duke University
Set your CLASSPATH according to instructions in
/cs/cs60/help/JFLAP
then run
java JFLAP
The set of sequences accepted by an acceptor A is represented
L(A)
the "language of" A
A language L accepted by some finite-state acceptor is called a finite-state language.
Capabilities of finite-state machines are conveniently characterized
by the langueages they accept.
Do there exist non-finite-state languages?
Finite-State Machines can't count arbitrarily
high
are two examples of non-finite-state languages.
Suppose
were finite-state.
Let A be a finite-state acceptor for it.
Let N = # of states of A.
We can "trick" A into giving the wrong answer.
Consider the input sequence to A:
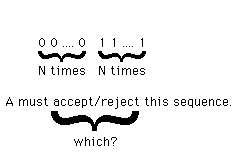
Consider the states A goes through in processing this input.
{ q0,
q1, ....,
qN} must
contain the same state, say qi, twice (or more).
There are only N states in the machine.

Let's short the original sequence by "splicing out" this inner sequence of 0's.
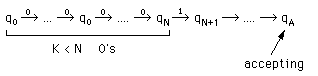
A also accepts
But this sequence is not in our language
Our supposition that the language is finite-state was wrong.
A way of saying that
L is finite-state
implies
Finite-state languages are "closed under complement"
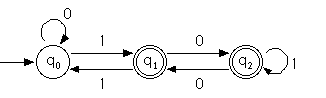
Example
Acceptor accepting numerals (MSB first) not divisible by 3
Other closure
properties of finite-state languages:
Example
L1 = all sequences of 0's & 1's with at least 2 1's
L2 = all sequences in which each 1 is immediately preceded by a 0
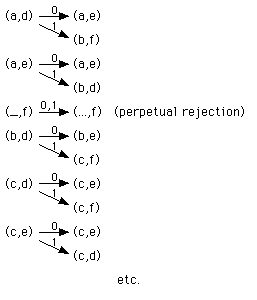
Diagram for the Intersection Machine
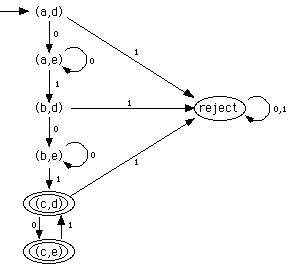
operating in parallel
with "cross-connections" between machines
"Regular Expressions" characterize finite-state languages precisely.
A regular expression is like a one-line, non-recursive grammar.
* is often used where we used {...} before
e.g.
{ 0 | 1 } 11
would be
( 0 | 1 )* 11
Every regular expression is built up from
(0|1)*11
denotes seqences of 0's & 1's ending
in 11
0*10*10* sequences with exactly two 1's
(0*10*10*)* sequences with an even number of 1's
(0|1)*01101(0|1)* seqences containing a 01101
Regular Expressions have their own algebraic laws :
etc.
Regular Expressions represent paths on directed labeled graphs :
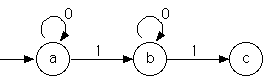
The paths from a to c are succinctly represented
0*10*1