Monte-Carlo explorations of purchase strategies

Based on a combination of innate cynicism and having made some very good purchases during recessions, I have been disinclined to buy much in the past few years. But it has become apparent to me that waiting for a 25% drop has caused me to miss 50% gains. These simulations are an effort to moderate my instincts with data.

• I obtained 150 years of (monthly) S&P500 data from DataHub.io's CSV version of Robert Shiller's data.
• I built a Monte-Carlo simulator that could return (appreciation, dividend, interest rate) tupples, either from randomly chosen months or as real sequences chosen from random periods.
• I implemented a few buying-strategy simulators that could be executed against simulated markets:
  • Two base cases: All-In (buy everything on day one) and All-Out (keep everything in CDs).
  • The (vanilla) Continuous Purchase ... buy positions, once a year, on January first. Spreading that out over from one to five years.
  • At the opposite extreme Bottom Buying ... wait for the absolute market low, and possibly a few lesser lows leading up to it.
  • My personal favorite Buying the Dips ... targeting drops between 10-25%, and optional gradual buy-ins (e.g. 1/4 at 10%, 1/2 at -15% and the rest at -20%).

Caveats

The distributions are wide and the standard deviations are, in most interesting cases, similar to (or even greater than) the mean values. There are clearly no guarantees, and results are much more dependent on the market than strategy.

The S&P500 data I used had only monthly data. This likely under-estimates the performance of both Bottom and Dip buying, as the actual bottoms are unlikely to have ocurred on the first of a month.

I chose to base my simulations on 1950-2018 data. It could be argued that the next twenty years will be fundamentally unlike the last seventy.

Summary

I ran each of these strategies against a large number of actual market histories (20 year snippets starting at various times), plotted the distribution of results, and reported the measured means and standard deviations. The resulting distributions and statistics are below. My attempted summary of these results and their lessons is:

1. The (sanity check) All-In and All-Out strategies yielded results that were very consistent with the historical ranges of interest rates, appreciations, and dividends.
2. The Continuous Purchase models returned only 50-60% as much as All-In, but with a lower standard deviation. This seems reasonable because:
   • the general trend of the market is up, so delaying purchases for 2-5 years means missing out on 2-5 years of appreciation ... which is about the difference in return.
   • a single purchase might happen to be in a very good or a very bad year. Spreading the purchase out over a few years will moderate those extremes, reducing the standard deviation.
3. The (omniscient) Bottom-Buying implementation achieved the highest mean returns, but also had the highest standard deviation. In many cases we had to wait so long (for the bottom) that the lost appreciation greatly outweighed the gained bargain. Progressive Bottom Buying (buying a bit at earlier-but-lesser bottoms) seemed as likely to hurt the return (gain less of a bargain) as help it (put some money to work sooner). True bottoms are few and far-between. If you happen to catch a bottom early in the process, it can be very profitable; But that is not a likely outcome.

   It should be noted that the Bottom-Buying implementation is not a real strategy, as it inspected the entire 20 years before deciding when to buy. It was only included as a stadard against which other (possible) strategies could be evaluated.

4. Buying the Dips seemed to suffer similar greed penalties:
   • Waiting for 20-25% dips lowered our mean returns ... presumably because of how long we have to wait for them.
   • Progressive purchase (e.g. 1/4 at -10%, 1/2 at -15%, rest at -20%) improved our mean returns ... likely due to a combination of (a) putting money to work sooner and (b) mitigating the cost if -20% never comes.

5. I observed that all strategies performed better when run against randomly chosen results, rather than randomly chosen sequences. I infer this to have been because the former did not include long periods of good or poor performance ... which challenge most of the buying strategies. Sadly, the number of randomly chosen sequences is much smaller than the number of randomly chosen combinations, so the training data is much thinner when used in this more realistic way.

The training data is thin, and all results had high standard deviations, but to the extent that these results can make recommendations, the best strategy might be:

buy 30-50% on a 5% dip and the rest on a 10% dip (mean=21)

buy 30-50% on a 10% dip and the rest on a 15% dip (mean=18.5)

Results

	All-In/Out CDs, 20 years: mean=3.10, sigma=1.41
	All-In/Out market, 20 years: mean=12.92, sigma=15.96
	

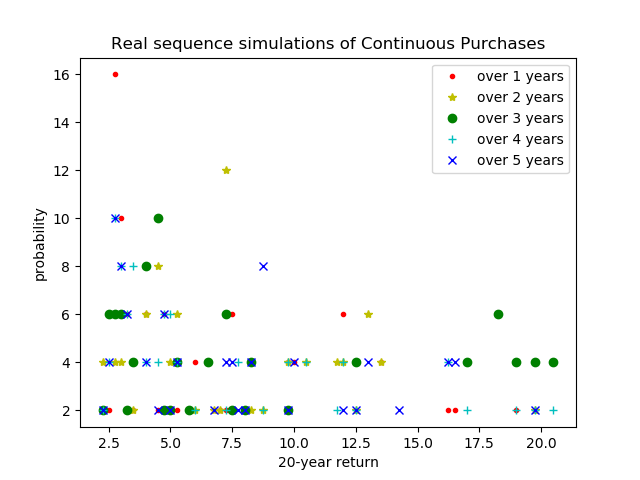
	Continuous Purchases over 1 years, 20 years: mean=6.86, sigma=4.59
	Continuous Purchases over 2 years, 20 years: mean=8.18, sigma=4.58
	Continuous Purchases over 3 years, 20 years: mean=8.34, sigma=6.16
	Continuous Purchases over 4 years, 20 years: mean=7.10, sigma=5.10
	Continuous Purchases over 5 years, 20 years: mean=7.49, sigma=4.60
	

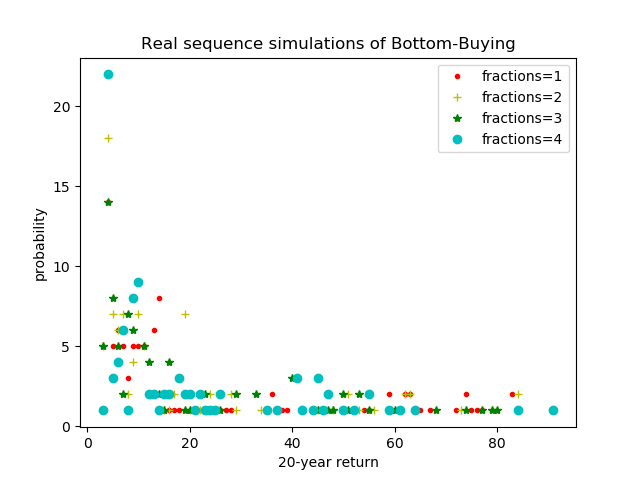
	Bottom-Buying over 20 years in 1 pieces: mean=23.58, sigma=24.29
	Bottom-Buying over 20 years in 2 pieces: mean=19.10, sigma=20.27
	Bottom-Buying over 20 years in 3 pieces: mean=20.95, sigma=20.71
	Bottom-Buying over 20 years in 4 pieces: mean=19.61, sigma=19.24
	

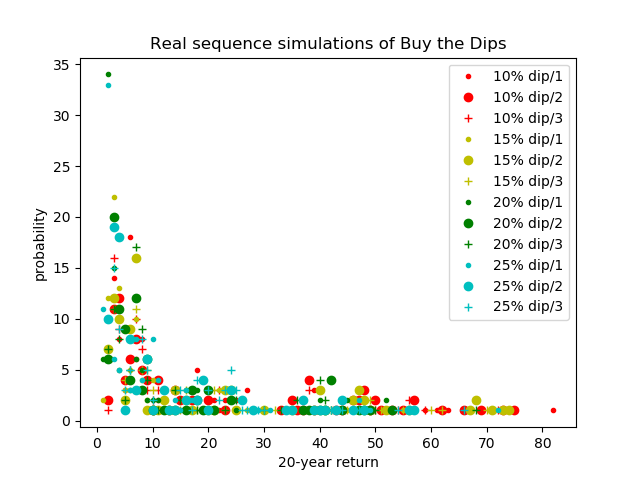
	Buy the Dips(10%/1) over 20 years: mean=13.77, sigma=15.73
	Buy the Dips(10%/2) over 20 years: mean=21.09, sigma=20.62
	Buy the Dips(10%/3) over 20 years: mean=18.39, sigma=19.22

	Buy the Dips(15%/1) over 20 years: mean=10.48, sigma=11.95
	Buy the Dips(15%/2) over 20 years: mean=18.50, sigma=19.95
	Buy the Dips(15%/3) over 20 years: mean=17.61, sigma=18.86

	Buy the Dips(20%/1) over 20 years: mean=10.05, sigma=13.70
	Buy the Dips(20%/2) over 20 years: mean=12.46, sigma=13.43
	Buy the Dips(20%/3) over 20 years: mean=14.47, sigma=14.10

	Buy the Dips(25%/1) over 20 years: mean=9.66, sigma=13.31
	Buy the Dips(25%/2) over 20 years: mean=13.16, sigma=14.05
	Buy the Dips(25%/3) over 20 years: mean=13.88, sigma=13.24