CS 60 Final with Answers, Spring 1997

Your name __________________________

Harvey Mudd College

CS 60 Final Exam

Spring semester, 1997

Closed book

3 hours

8 problems

8 pages

The exam is given under the conditions of the HMC honor code. Consulting with others during the examination is forbidden. You are allowed to use one 8.5" x 11" sheet of your own notes, but no other reference materials.

Please provide solutions to the attached problems directly on these pages. It is suggested that you look over the exam first to get an idea of how to apportion your time. Work so as to maximize total points. Do not get stuck on one problem at the expense of others.

The action items in each problem are shown in bold-face.

Use the back of the previous page if you need more space for a given problem.

There is virtue in concise answers. Think before you write.

1. [10 points]

[Warm-up, 1 point each]. Provide an answer for each question.

a. The number of different switching functions of n variables is:

b. Give an anonymous functional expression (using =>) for the following: The function which, with argument f, returns the function which, with argument X, returns the result of applying f to the result of applying f to X:

c. A program has to process each arc of an (unlabeled) directed graph with N nodes. Assuming the cost of processing a single arc is O(1), the cost to process the entire graph is upper-bounded by what function of N (using O notation):

d. Describe the way in which you remember the logical meaning of "implies".

e. Suppose that person is a 3-ary predicate, such that person(Name, Eyes, Hair) relates a person's name to her/his eye and hair color. Give a Prolog query which gives as a list the set of Names of persons with blue eyes and brown hair.

f. What is the significance of the linear addressing principle in algorithm design?

g. How is inheritance used to the programmer's advantage in the Java awt (abstract window toolkit)?

h. Give an example of a language which is not acceptable by any finite-state acceptor.

i. How many nodes are there in a perfectly-balanced binary tree of height h?

j . Translate the following loop using McCarthy's transformation. Assume that X is the input variable and Z is the result. Let the function computed be named f.

Z = 0;

for( Y = 0; Y < X; Y++)

    Z = Z + 2*Y + 1;

2. [15 points]

Write a short essay describing how you would use the object-oriented features of Java to build a library for describing hardware systems at the finite-state machine (e.g. register) level. Identify classes you would use and their methods. If possible, give an example of how you would code elements of a simple system involving register transfers and arithmetic. Note that by register transfers I am not referring to machine-language or assembly language (which are software), but rather a hardware interconnection of registers and other functional units.

3. [10 points]

Using an appropriate loop invariant, prove the partial correctness of the following program with respect to the assertions shown. Assume that all variables are integer.

input: x == x0  y == y0  x0 >= 0

prod = 0;

while( x > 0 ) 
  { 
  prod = prod + y; 
  x = x - 1; 
  }

output: prod == x0 * y0

Here x0 and y0 are variables serving to anchor the initial values of x and y, but which are not used in the program proper. In your proof of the loop verification condition, use primes to differentiate the values of variables after the loop body.

4. [15 points]

Consider developing a function which tests two lists for being equal-as-sets, meaning that they have the same elements without regard to repetition and order. For example, the pair of lists on the left are equal-as-sets, whereas the pair on the right are not:

[3, 1, 2, 1, 5] vs. [1, 2, 3, 5]     [1, 2, 3] vs. [2, 3, 4]

Although the lists won't necessarily contain numbers as elements, assume throughout that two elements can be compared for == and for < in O(1) time. Consider three possible implementations for equal-as-sets:

a. Use two nested loops which range over the two lists, searching the second list once for every element of the first list to see whether the element lies in the second list, or vice-versa.

b. Sort the two lists first and remove duplicates, then check to see whether the lists are identical by comparing them point-by-point. (Don't give the algorithms themselves; just state reasonable assumptions.)

c. Build a hash table for the elements of each list. For each element of the first list, check to see whether it is in the table of the second and vice-versa. (Assume that each check is O(1).)

Give an "O" complexity comparison of these three methods for testing equality-as-sets, assuming for simplicity that both lists have the same number, N, of elements.

5. [10 points]

In the following program, assume that P has constant run-time regardless of the argument values.

for( int k = 1; k <= N; k = k*2 )

  for( int i = k; i > 0; i = i/2 )

    for( int j = 0; j < i; j++ )

      P(i, j, k);

As a function of the value of N, derive the tightest possible "O" bound on the run-time. Explain your derivation; don't just give an answer.

6. [20 points]

A chronograph (i.e. "stop watch") has an overall design as shown in the following diagram:

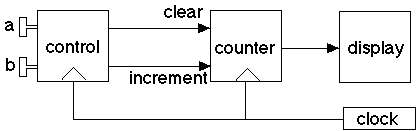
The control and counter are finite-state machines. Counter is simply a register with two strobes: clear and increment. Clear resets the value of the counter to 0 and increment causes it to be incremented on each clock tick.

The control machine works as follows: There are two buttons, a and b, either or both of which are assumed to be pressed (1), or not-pressed (0) when the clock ticks. The control has four states: reset, run, stop, and stop2. The control starts in the reset state. In any state, if button a is being held down, the machine invariably goes to the run state. If the machine is in the run state and button b is held down (but button a is not) it goes to the stop state. The machine stays in the stop state until button b is released, at which point it goes to the stop2 state. From the stop2 state, if button b is pressed, the machine goes to the reset state, where it stays when the button is released. Thus the purpose of the stop2 state is to prevent the machine from immediately leaving the stop state and going to the reset state as a result of button b being held down; button b must be released once before this can happen.

The effect of the control on the counter is as follows: In the run state, the increment strobe is activated, enabling the counter to count upward with each clock tick. In the reset state, the clear strobe is activated, which resets the counter. In the stop and stop2 states, neither strobe is activated, so the counter retains its previous value.

a. [5 of 20] Give the state diagram for the control. For each state, your diagram should account for the four input possibilities.

b. [5 of 20] Assume the following 2-flip-flop (u and v, say) encoding of states: reset = 00, run = 01, stop = 11, stop2 = 10. Show the state-transition table for the control in the form of a pair of Karnaugh maps, with the rows of the table corresponding to states and the columns corresponding to the button combinations. These will be 4-variable maps, since there are two buttons and two state variables.

c. [10 of 20] Show a simplified logic implementation of the control machine and the connection to the counter.

7. [10 points]

Suppose we wish to use the ISC architecture to add up the elements in a linked list. Assume that the list cells are as follows, where n is a typical location:

Location n contains the datum in the cell.

Location n+1 contains the address of the next cell in the list.

A contained address of 0 indicates the end of the list.

For example, we might have a list representing [5, 6, 7, 8, 10, 11] with first cell in location 100, and other relevant cells as shown below:

loc'n contents 	   loc'n contents

100: 5 			106: 10

101: 110		107: 104

102: 7 			108: 8

103: 108 		109: 106

104: 11 		110: 6

105: 0 			111: 102

Note that the list elements are not in order by increasing storage location; with a linked list they need not be. Assuming that rest is a register already initialized to the address of the first cell in the list, write ISCAL code which will leave the sum of the list elements in a register sum.

You may assume that the initial contents of rest need not be preserved. Introduce any additional registers which you feel are necessary. An iterative, rather than recursive, solution is strongly suggested.

The following are mnemonics from the ISC repertoire:

lim R C 	load immediate register R constant C

aim R C 	add immediate register R constant C

copy R S 	copy register S into register R

add R S T	put the sum of register S and register T into register S

load R S 	load the contents of memory location in register S into register R

store R S	store into the memory location in register R the value in register S

jeq R S T	jump to the location in register R if the contents of register S equals that of register T

junc R 		jump unconditionally to the location in register R

8. [10 points]

An equivalence relation is a special type of binary relation for which an information structure known as a partition is a possible representation. A partition is simply a list of non-empty lists with the property that no element occurs in more than one of the lists. For example,

[ [1, 3, 6], [2, 5], [4], [7, 8] ] is a partition

[ [1, 3, 7], [2, 5], [4], [6, 7, 8] ] is not a partition (7 occurs in two lists)

[ [1, 3, 7], [ ], [4], [6, 8] ] is not a partition (one of the lists is empty)

The way in which a partition represents a binary relation is as follows: two elements are related if, and only if, they both occur in a common element of the partition. Taking the following list as an example of the partition:

[ [1, 3, 6], [2, 5], [4], [7, 8] ]

2 is related to 5, since they both occur in the second element of the partition

2 is related to 2, for the same reason

2 is not related to 4, since they do not occur in a common element of the partition

Give a functional program defining the function related such that related(P, i, j) is true exactly when i is related to j according to partition P. You may use recursion or any higher-order functions which you can remember or wish to define.

Try to make your answer as simple and elegant as possible.